Integer Programming: Macro Optimization Model
Tl;dr: I've tried many diets and decided to use a MILP to help me stick to my macros whenever I order from Sweetgreen.
Background
Dieting amiright? I've tried Keto, Paleo, veganism, vegetarianism, intermittent fasting, you name it. Lately, my diet has been largely vegan, but not on purpose. Berlin has so many vegan restaurants and options, it is so easy… too easy. But every month I desperately crave a burger from Burgermeister and just try to stop me from getting it.
Through exploring different diets and foods, I noticed I was essentially solving little food puzzles. Close to my office in Boston, there was a Sweetgreen that was super popular. I may have gone there once a week? I knew people who went there every day.
While dieting, I had to figure out what meal I could get from this establishment that would satisfy my macros. I was calculating it manually using the MyFitnessPal app by adding different salads and seeing what I had left for the day then removing it and trying another salad seeing what made the most sense. One afternoon, I decided that this was a silly waste of time. So, I created a model to make the decision for me.
BMR Calculator
When I started learning about nutrition, the first thing I was told to calculate my Basal Metabolic Rate (BMR), which is the number of calories you burn a day just by existing:
Calculator 1
Calculator 2
Calculator 3
I provided three because every calculator is a little different. I took the average of the three and got about 1500 calories. So if I didn't move my body all day, I need at least 1500 calories to maintain my bodily functions. While recovering from knee surgery, I understand this lifestyle more than I care to admit.
Caloric Intake Calculation
Now I want to know how many calories I should eat to maintain my weight, gain weight, or lose weight. Again, I'll provide a few.
Calculator 1
Calculator 2
Calculator 3
I checked that my targeted caloric intake was greater than my BMR.
Macro Mix
On average, carbohydrates and protein contain 4 calories per gram, fats contain 9 calories per gram, and alcohol has 7 calories per gram.[1]
The acceptable macronutrient distribution ranges (AMDR)[2] for my age and sex group are:
Protein: 10-35%
Carbs: 45-65%
Fats: 20-35%
I messed around with these percentages for years until I found a mix that worked well for me. I currently aim for about 30% Protein, 50% Carbs, 20% Fats.
Calorie Tracking
With my calorie tracking app, I submitted my target calorie amount and my macro percentages. The reason this program works is that the input to the model is the remaining volume of macros at the time I get a salad. The optimization will pick the salad that best matches the distribution of the remaining macros. This is because we will build the objective function to minimize the distance between all of the target macros and the macros in each menu item.
Premade Salad Model
Input
I started by grabbing the nutritional information from the sweetgreen site:
Sweetgreen Nutritional Information
I used a pdf to csv converter to create an input file. I rearranged the rows and added a category column to make it easier to separate different menu options.
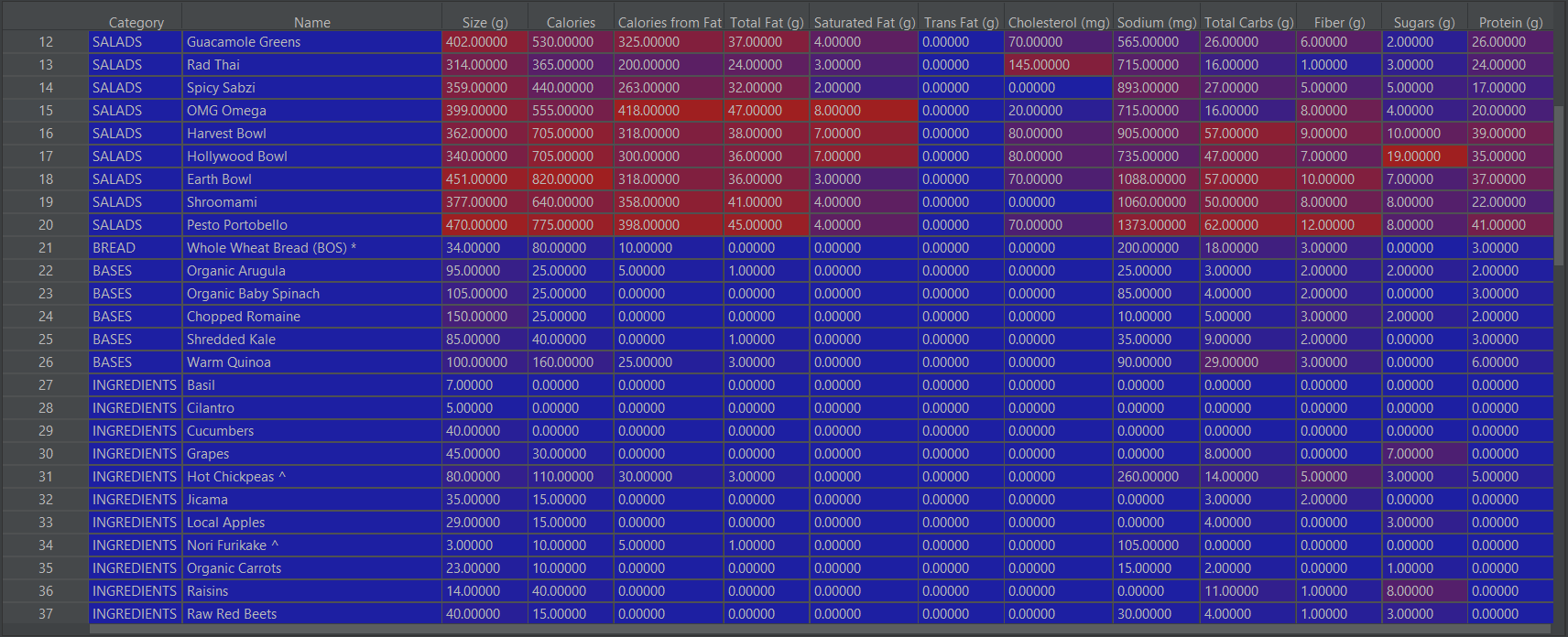
We also want to include our macro targets P, C and F.
Objective Function
We want to fulfill as many macros as possible with our salad selection. Using our macro targets P, C and F, we minimize the distance between the salad selection nutrients and the targets. This is demonstrated mathematically below. $$\min \sum\limits_{i \in Salads} (P - p_ix_i) + (C - c_ix_i) + (F - f_ix_i)$$ $$\min (P + C + F)-\sum\limits_{i \in Salads} p_ix_i + c_ix_i + f_ix_i$$ $$\min (P + C + F)-\sum\limits_{i \in Salads} (p_i + c_i + f_i)x_i$$
Constraints
We can only choose one salad: \(\sum\limits_{i \in Salads} x_i = 1\)
We do not want to exceed our macro limits:
Protein maximum: \(\sum\limits_{i \in Salads} p_ix_i \leq P\)
Carbohydrate maximum: \(\sum\limits_{i \in Salads} c_ix_i \leq C\)
Fat maximum: \(\sum\limits_{i \in Salads} f_ix_i \leq F\)
Binary Variables: \(x_i = bin\) \(\forall i \in Salads\)
PuLP and Gurobi
To solve linear programs with Python, we utilize the PuLP package. To install and import pulp, I use pip:
pip install pulp
You can test pulp by entering a python environment and running pulp.pulpTestAll() from the command line:
python
Import pulp
pulp.pulpTestAll()
We have the first solver available but can add other solvers like gurobi by running:
python -m pip install -i https://pypi.gurobi.com gurobipy
Running pulp.pulpTestAll() should now show that gurobi as available.
Premade Salad Selection Code
import pulp
import pandas as pd
#import nutritional csv
menu = pd.read_csv('./sweetgreen_PP.csv')
menu = menu.dropna()
#pull out the premade salads
salads = menu[menu['Category'] == 'SALADS'].copy()
#Instantiate the model
model = pulp.LpProblem("MacroModel", pulp.LpMinimize)
#Set variable names
salad_names = list(salads['Name'])
#Set decision variables as Binary 0 or 1
x = pulp.LpVariable.dicts("x", salad_names, cat='Binary')
#Build objective function
zp = dict(zip(salad_names, salads['Protein (g)'])) #protein
zc = dict(zip(salad_names, salads['Total Carbs (g)'])) #carbs
zf = dict(zip(salad_names, salads['Total Fat (g)'])) #fats
#Set Macro limits (For Example)
P = 37
C = 90
F = 35
#Set Objective Function:
model += (P + C + F) - pulp.lpSum([(zp[i] + zc[i] + zf[i] ) * x[i] for i in salad_names])
#Add Constraints
model += pulp.lpSum([x[i] for i in salad_names]) == 1, 'Salad Limit'
model += pulp.lpSum([(x[i] * zp[i]) for i in salad_names]) <= P, 'Protein Max'
model += pulp.lpSum([(x[i] * zc[i]) for i in salad_names]) <= C, 'Carb Max'
model += pulp.lpSum([(x[i] * zf[i]) for i in salad_names]) <= F, 'Fat Max'
#set solver
solver = pulp.getSolver('GUROBI')
# Solve model
model.solve(solver)
#Print Status
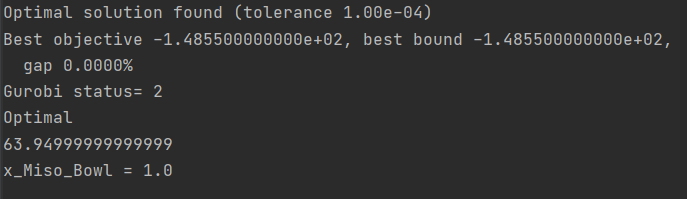
print(pulp.LpStatus[model.status])
#Print Objective Value
print(pulp.value(model.objective))
#Print decision variables and get name of chosen salad
for i,v in enumerate(model.variables()):
if(v.varValue > 0):
print(v.name, "=", v.varValue)
name = v.name.split('x_')[1].replace("_", " ")
Output
Build Your Own Salad
Sweetgreen, along with so many other establishments, lets you build your own creation using a set of ingredients and rules such as "Pick up to two bases/ four ingredients/ up to two premiums/ etc." We can adapt the logic from the premade salad model to this model. Then, we can combine our two models to tell us FINALLY what I should order at Sweetgreen.
BYO Salad Code
# pull out the build your own ingredients
ingredients = menu[menu['Category'] != 'SALADS'].copy()
# Instantiate the model
model = pulp.LpProblem("MacroModel", pulp.LpMinimize)
# Set variable names
indices = list(zip(ingredients.Category, ingredients.Name))
# Set decision variables as Binary 0 or 1
x = pulp.LpVariable.dicts("x", indices, cat='Binary')
# Build objective function
zp = dict(zip(indices, ingredients['Protein (g)'])) # protein
zc = dict(zip(indices, ingredients['Total Carbs (g)'])) # carbs
zf = dict(zip(indices, ingredients['Total Fat (g)'])) # fats
# Set Objective Function:
model += (P + C + F) - pulp.lpSum([(zp[i] + zc[i] + zf[i]) * x[i] for i in salad_names])
# Add Constraints
model += pulp.lpSum([(x[i] * zp[i]) for i in indices]) <= P, 'Protein Max'
model += pulp.lpSum([(x[i] * zc[i]) for i in indices]) <= C, 'Carb Max'
model += pulp.lpSum([(x[i] * zf[i]) for i in indices]) <= F, 'Fat Max'
br = [(k[0],k[1]) for k, v in x.items() if k[0] == 'BREAD']
model += pulp.lpSum([x[(i,j)] for i,j in br]) <= 1, 'Bread Limit'
bs = [(k[0], k[1]) for k, v in x.items() if k[0] == 'BASES']
model += pulp.lpSum([x[(i, j)] for i, j in bs]) <= 2, 'Base max'
model += pulp.lpSum([x[(i, j)] for i, j in bs]) >= 1, 'Base min'
ing = [(k[0], k[1]) for k, v in x.items() if k[0] == 'INGREDIENTS']
model += pulp.lpSum([x[(i, j)] for i, j in ing]) <= 4, 'Ingredient Limit'
pr = [(k[0], k[1]) for k, v in x.items() if k[0] == 'PREMIUMS']
model += pulp.lpSum([x[(i, j)] for i, j in pr]) <= 2, 'Premium Limit'
dr = [(k[0], k[1]) for k, v in x.items() if k[0] == 'DRESSINGS']
model += pulp.lpSum([x[(i, j)] for i, j in dr]) <= 2, 'Dressing Limit'
bv = [(k[0], k[1]) for k, v in x.items() if k[0] == 'BEVERAGES']
model += pulp.lpSum([x[(i, j)] for i, j in bv]) <= 1, 'Beverages Limit'
#set solver
solver = pulp.getSolver('GUROBI')
# Solve model
model.solve(solver)
#Print Status
print(pulp.LpStatus[model.status])
#Print Objective Value
print(pulp.value(model.objective))
#Print decision variables and get name of chosen ingredients
solution = list()
for v in model.variables():
if(v.varValue > 0):
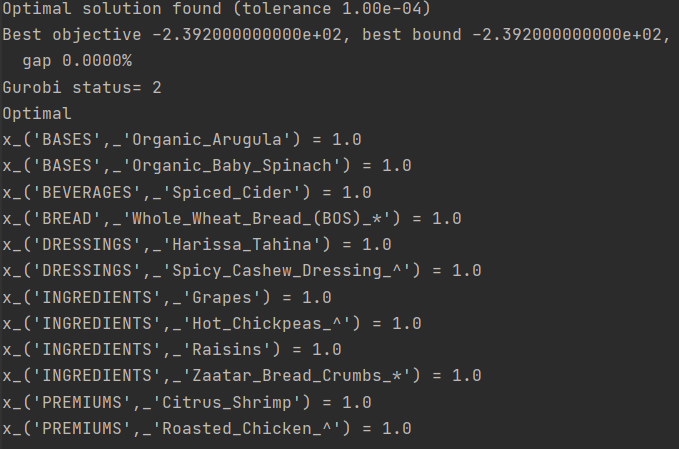
print(v.name, "=", v.varValue)
name = v.name.split('x_')[1].replace("_", " ")
name = name.split("', '")[1]
name = name.split("')")[0]
solution += [name]
Output
Ok, now we can combine everything. I'm aware there must be a solution that involved a constraint using a min() function that can combine both models seamlessly, but I already have the code for both so I combined it such that the overall opt runs multiple optimizations. That was the easiest way for my to think about it in terms of pulp.
Overall Salad Code
import pulp
import pandas as pd
from premade_salad_opt import *
from byo_salad_opt import *
def full_menu_model(P, C, F):
# import nutritional csv
menu = pd.read_csv('./sweetgreen_PP.csv')
menu = menu.dropna().reset_index(drop = True)
# set solver
solver = pulp.getSolver('GUROBI')
#Start by getting the best premade salad
premade_model = premadesalad_selection(P, C, F)
premade_model.solve(solver)
premade_solution = pm_postprocess(premade_model)
#Parse out winning premade salad and save for later
pm = menu[menu['Name'] == premade_solution].copy()
# run build your own BYO salad model
byo_model = byo_salad_model(P, C, F)
byo_model.solve(solver)
byo_solution = byo_postprocess(byo_model)
#Parse out the BYO solution then condense it down to one salad
byo = menu[menu['Name'].isin(byo_solution)].copy()
condensed_byo = pd.DataFrame(byo.iloc[:,2:].sum()).T
condensed_byo['Name'] = 'BYO'
condensed_byo['Category'] = 'BYO'
#combine the two leading contenders
full_menu = pm.append(condensed_byo)
# Instantiate the full model
model = pulp.LpProblem("MacroModel", pulp.LpMinimize)
# Set variable names
salad_names = list(full_menu['Name'])
# Set decision variables as Binary 0 or 1
x = pulp.LpVariable.dicts("x", salad_names, cat='Binary')
# Build objective function
zp = dict(zip(salad_names, full_menu['Protein (g)'])) # protein
zc = dict(zip(salad_names, full_menu['Total Carbs (g)'])) # carbs
zf = dict(zip(salad_names, full_menu['Total Fat (g)'])) # fats
# Set Objective Function:
model += (P + C + F) - pulp.lpSum([(zp[i] + zc[i] + zf[i]) * x[i] for i in salad_names])
# Add Constraints
model += pulp.lpSum([x[i] for i in salad_names]) == 1, 'Salad Limit'
model += pulp.lpSum([(x[i] * zp[i]) for i in salad_names]) <= P, 'Protein Max'
model += pulp.lpSum([(x[i] * zc[i]) for i in salad_names]) <= C, 'Carb Max'
model += pulp.lpSum([(x[i] * zf[i]) for i in salad_names]) <= F, 'Fat Max'
model.solve(solver)
full_solution = full_postprocess(model)
if full_solution == 'BYO':
solution = byo_solution
else:
solution = premade_solution
return solution
if __name__ == '__main__':
#Set Macro limits
P = 37
C = 120
F = 35
#import nutritional csv
menu = pd.read_csv('./sweetgreen_PP.csv')
menu = menu.dropna()
#Run full model
solution = full_menu_model(P, C, F)
# Parse out the Overall solution then condense it down to one salad
result = menu[menu['Name'].isin(solution)].copy()
condensed_result = pd.DataFrame(result.iloc[:, 2:].sum()).T
rP = condensed_result['Protein (g)'].sum()
rC = condensed_result['Total Carbs (g)'].sum()
rF = condensed_result['Total Fat (g)'].sum()
#Print Results
print('Final Salad:', solution)
print("Target Protein: {} "
"Salad Protein: {} "
"Remaining Protein: {}".format(P, rP, P - rP))
print("Target Carbs: {} "
"Salad Carbs: {} "
"Remaining Carbs: {}".format(C, rC, C - rC))
print("Target Fat: {} "
"Salad Fat: {} "
"Remaining Fat: {}".format(F, rF, F - rF))
Output
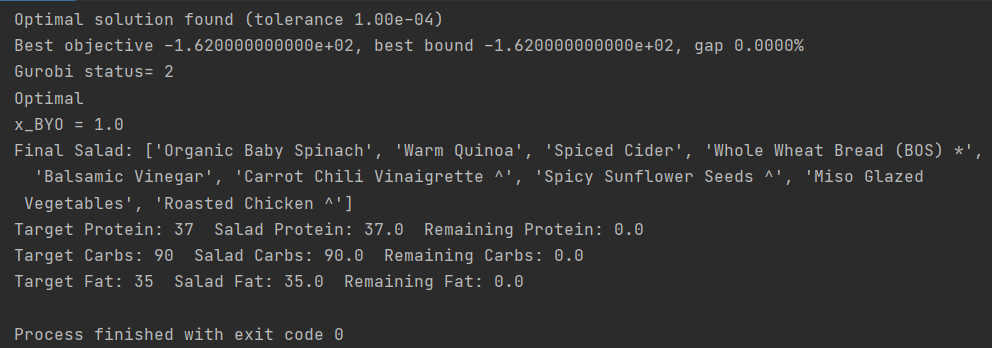
Model Behavior
The model definitely favors building your own salad. That is because it has many more small pieces to work with in order to build up to approach target macro values more accurately than the premade salads.
Forging Ahead
I had an early version of this model years ago that had a cost component. Since then I have lost the data file that contains the costs associated with each menu item from Sweetgreen. When I had it, I included a cost component into the optimization and it made some pretty interesting selections!
I love this project because it combines nutrition, something I learned about later in life following a childhood of eating mostly pasta and Cheetos), and linear programming, which is truly a passion of mine.
[1] U.S. Department of Health and Human Services and U.S. Department of Agriculture. 2015 ‐ 2020 Dietary Guidelines for Americans. 8th Edition. December 2015. Available at https://health.gov/our-work/food-nutrition/previous-dietary-guidelines/2015.
[2] Appendix E-3.1.A4 | health.gov. (2015). Appendix E-3.1.A4. Nutritional Goals for Each Age/Sex Group Used in Assessing Adequacy of USDA Food Patterns at Various Calorie Levels. https://health.gov/our-work/food-nutrition/previous-dietary-guidelines/2015/advisory-report/appendix-e-3/appendix-e-31a4